
1. In quadrilateral ABCD, AC = AD and AB bisects ∠A (see Fig. 7.16). Show ` \▵ABC≅▵ABD\ `. what can you say about BC and BD?

solution :
Given,
AC = AD and AB bisect ∠A.
Find,
` \▵ABC≅▵ABD\ `
BC and BD
In the Fig,
AB bisect ∠A[ Given ]
` \=>∠BAC=∠BAD\ `
Now,
In ` \▵ABC\ ` and ` \▵ABD\ `,
AC = AD[ Given ]
∠CAB = ∠DAB[ Given ]
AB = AB[ Common ]
So,
` \▵ABC≅▵ABD\ `[ SAS rule ]
Then,
BC = BD[ CPCT ]
I say about BC and BD is equal.
2. ABCD is a quadrilateral in which AD =
BC and ∠DAB = ∠CBA (see Fig. 7.17). Prove that
(i) ` \▵ABD≅▵BAC\ `
(ii) BD
= AC
(iii) ∠ABD = ∠BAC.

solution :
Given,
AD = BC and ∠DAB = ∠BAC,
Find,
(i) ` \▵ABD≅▵BAC\ `
(ii) BD
= AC
(iii) ∠ABD =
∠BAC.
Now,
In ` \▵ABD\ ` and ` \▵BAC\ `,
AD = BC[ Given ]
∠DAB = ∠CBA[ Given ]
AB = AB[ Common ]
So,
(i) ` \▵ABD≅▵BAC\ `[ SAS rule ]
(ii) BD = AC[ CPCT ]
(iii) ∠ABD = ∠BAC[ CPCT ]
3. AD and BC are equal perpendiculars to a line segment AB (see Fig. 7.18). Show that CD bisects AB.

solution :
Given,
AD = BC and ∠CBO = ∠DAO.
Find,
CD bisect AB,
In the Fig,
BC and AD are perpendicular AB.
We say,
BC ` \||\ ` AD
CD is a transversal line.
∠BCD = ∠ADC` \-----(I)\ `[ Alternate interior angles ]
Now,
In ` \▵CBO\ ` and ` \▵DAO\ `,
∠BCD = ∠ADO[ From (I) ]
BC = AD[ Given ]
∠CBO = ∠DAO[ Given ]
so,
` \▵CBO≅▵DAO\ `[ ASA rule ]
Then,
BO = AO[ CPCT ]
CO = DO[ CPCT ]
Now,
I say that CD bisects AB.
4. ` \l\ ` and ` \m\ ` are two parrel lines intersected by another pair of parallel lines ` \p\ ` and ` \q\ ` (see Fig. 7.19). Show that ` \▵ABC≅▵CDA\ `.

solution :
Given,
l ` \||\ ` m and p ` \||\ ` q.
Find,
` \▵ABC≅▵CDA\ `
In the Fig,
l ` \||\ ` m and AC is a transversal line.
∠DAC = ∠BCA` \-----(I)\ `[ Alternate interior angles ]
∠BAC = ∠DCA` \-----(II)\ `[ Alternate interior angles ]
Now,
In ` \▵ABC\ ` and ` \▵CDA\ `,
∠BAC = ∠DCA[ From (I) ]
AC = AC[ Common ]
∠BCA = ∠DAC[ From (II) ]
So,
` \▵ABC≅▵CDA\ `[ ASA rule ]
5. Line ` \l\ ` is the bisector of an angle
∠A and B is any point on ` \l\ `. BP and BQ are perpendiculars
from B to the arms of ∠A (see Fig. 7.20). Show that:
(i) ` \▵APB≅▵AQB\ `
(ii) BP = BQ or B is equidistant from the arms of
∠A.
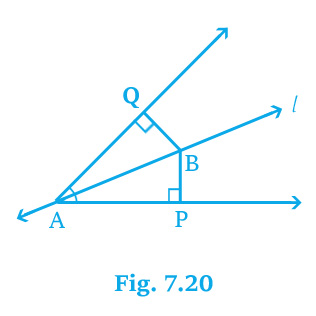
solution :
Given,
l bisect ∠A and BP and BQ are perpendiculars from B to the arms of ∠A.
Find,
(i) ` \▵APB≅▵AQB\ `
(ii) BP = BQ or B is equidistant from the arms of ∠A.
In the Fig,
l bisect ∠A[ Given ]
∠BAQ = ∠BAP` \-----(I)\ `
Now,
In ` \▵APB\ ` and ` \▵AQB\ `,
∠P = ∠Q[ 90° Given ]
∠BAP = ∠BAQ[ From (I) ]
AB = AB[ Common ]
So,
(i) ` \▵APB≅▵AQB\ `[ AAS rule ]
Now,
(ii) BP = BQ[ CPCT ]
So,
It can be said the point B is equidistant from the arms of A.
6. In Fig. 7.21, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.

solution :
Given,
AC = AE, AB = AD and ∠BAD = ∠EAC.
Find,
BC = DE
In the Fig,
∠BAD = ∠EAC[ Given ]
Add ∠DAC both side,
∠BAD + ∠DAC = ∠EAC + ∠DAC
⇒ ∠BAC = ∠EAD` \-----(I)\ `
Now,
In ` \▵ABC\ ` and ` \▵ADE\ `,
AB = AD[ Given ]
∠BAC = ∠EAD[ From (I) ]
AC = AE[ Given ]
So,
` \▵ABC≅▵ADE\ `[ SAS rule ]
Now,
BC = DE[ CPCT ]
7. AB is a line segment and P is its mid-point. D
and E are points on the same side of AB such that ∠BAD =
∠ABE and ∠EPA = ∠DPB (see Fig. 7.22). Show that
(i) ` \▵DAP≅▵EBP\ `
(ii) AD
= BE

solution :
Given,
AP = BP, ∠BAD = ∠ABE and ∠EPA = ∠DPB.
Find,
(i) ` \▵DAP≅▵EBP\ `
(ii) AD = BE
In the Fig,
∠EPA = ∠DPB[ Given ]
Add ∠EPD both side.
∠EPA + ∠EPB = ∠DPB + ∠EPD
⇒ ∠APD = ∠EPB` \-----(I)\ `
Now,
In `\ ▵DAP\ ` and ` \▵EBP\ `,
∠DAP = ∠EBP[ Given ]
AP = BP[ Given ]
∠APD = ∠EPB[ From (I) ]
So,
` \▵DAP≅▵FPB\ `[ ASA rule ]
Now,
AD = BE[ CPCT ]
8. In right triangle ABC, right angled at C, M is
the mid-point of hypotenuse AB. C is joined to M and produced to a point
D such that DM = CM. point D is joint B (see Fig. 7.23). Show
that:
(i) ` \▵AMC≅▵BMD\ `
(ii) ∠DBC
is a right angle.
(iii) `
\▵DBC≅▵ACB\ `
(iv) CM =`
\frac{1}{2}\ `AB

solution :
Given,
` \▵ABC\ ` is right angled triangle, ∠C = 90°, AM = BM and DM = CM.
Find,
(i) ` \▵AMC≅▵BMD\ `
(ii) ∠DBC is a right angle.
(iii) ` \▵DBC≅▵ACB\ `
(iv) CM =` \frac{1}{2}\ `AB
In ` \▵AMC\ ` and ` \▵BMD\ `,
AM = BM[ Given ]
∠AMC = ∠BMD[ Vertically opposit angles ]
CM = DM[ Given ]
So,
(i) ` \▵AMC≅▵BMD\ `[ SAS rule ]
∠ACM = ∠BDC[ CPCT ]
AC = BD` \-----(I)\ `[ CPCT ]
Now,
∠ACD = ∠BDC[ Alternate interior angles ]
So,
We say,
AC ` \||\ ` DB
In the Fig.
∠DBC + ∠ACB = 180°[ Co-interior angles ]
` \=>∠DBC + 90° = 180°\ `[ Given ∠C = 90° ]
` \=> ∠DBC=180°-90°\ `
` \=>∠DBC=90°\ `
(ii) ∠DBC is a right angle.
Now,
In ` \▵DBC\ ` and ` \▵ACB\ `,
BC = BC[ Common ]
∠DBC = ∠ACB[ right angles ]
DB = AC[ From (I) ]
So,
(iii) ` \▵DBC≅▵ACB\ `[ SAS rule ]
DC = AB[ CPCT ]
Now,
DM = CM[ Given ]
So,
DC = AB
⇒ DM + CM = AB
⇒ CM + CM = AB
⇒ 2 CM = AB
(iv) ` \CM=\frac{1}{2}AB\ `




0 Comments