
1. ` \▵\ `ABC and ` \▵\ `DBC
are two isosceles triangle on the same base BC and vertices A and D are
on the same side of BC (see Fig. 7.39). If AD is extended to intersect
BC at P, show that
(i) ` \▵ABD≅▵ACD\ `
(ii)
` \▵ABP≅▵ACP\ `
(iii) AP bisects ∠A as
well as ∠D.
(iv) AP is the perpendicular bisector of BC.

solution :
Given,
` \▵\ `ABC and ` \▵\ `DBC are isosceles triangle.
Find,
(i) ` \▵ABD≅▵ACD\ `
(ii) ` \▵ABP≅▵ACP\ `
(iii) AP bisects ∠A as well as ∠D.
(iv) AP is the perpendicular bisector of BC.
In ` \▵\ `ABD and ` \▵\ `ACD,
AB = AC[ Given ]
BD = CD[ Given ]
AD = AD[ Common ]
(i) ` \▵ABD ≅ ▵ ACD\ `[ Rule SSS ]
∠BAD = ∠CAD ` \-----(I)\ `[ CPCT ]
Now,
In ` \▵\ `ABP and ` \▵\ `ACP,
AB = AC[ Given ]
∠BAP = ∠CAP[ From (I) ]
AP = AP[ Common ]
(ii) ` \▵ABP ≅ ▵ ACP\ `[ Rule SAS ]
BP = CP ` \-----(II)\ `[ CPCT ]
Similarly,
In ` \▵\ `BDP and ` \▵\ `CDP,
BD = CD[ Given ]
DP = DP[ Common ]
BP = CP[ From (II) ]
` \▵BDP ≅ ▵ CDP\ `[ Rule SSS ]
∠BDP = ∠CDP ` \-----(III)\ `[ CPCT ]
From (I) and (III),
we say,
(iii) AP bisects ∠A as well as ∠D.
∠BPD + ∠CPD = 180°[ Linear pair of angles ]
⇒ ∠BPD + ∠BPD = 180°[ From (III) ]
⇒ 2 ∠BPD = 180°
⇒ ∠BPD = ` \frac{180°}{2}\ `
⇒ ∠BPD = 90°
As well as ∠CPD = 90°
From (II),
we say,
(iv) AP is the perpendicular bisector of BC.
2. AD is an altitude of an isosceles triangle ABC
in which AB = AC. Show that
(i) AD bisects BC
(ii) AD
bisects ∠A.
solution :

Given,
AD ⊥ BC and AB = BC
Find,
(i) AD bisects BC
(ii) AD bisects ∠A
In ` \▵\ `ADB and ` \▵\ `ADC
AB = AC[ Given ]
AD = AD[ Common ]
∠ADB = ∠ADC[ Given 90° ]
` \▵ADB≅▵ADC\ `[ Rule RHS ]
AD = CD[ CPCT ]
we say,
(i) AD bisects BC
∠BAD = ∠CAD[ CPCT ]
we say,
(ii) AD bisects ∠A.
3. Two sides AB and BC median AM of one triangle
ABC are respectively equal to sides PQ and QR and median PN of `
\▵\ `PQR (see Fig. 7.40). Show that:
(i) `
\▵ABM≅▵PQN\ `
(ii) `
\▵ABC≅▵PQR\ `

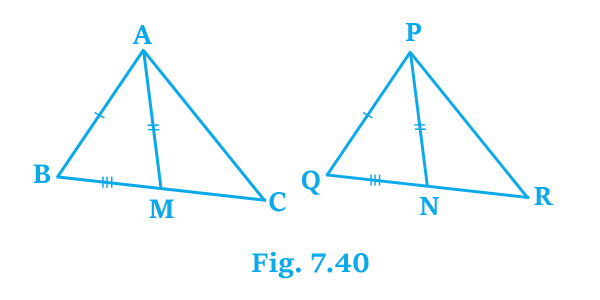
solution :
Given,
AB = PQ, BC = QR, AM = PN, BC median AM and QR median PN.
Find,
(i) ` \▵ABM≅▵PQN\ `
(ii) ` \▵ABC≅▵PQR\ `
In Fig.,
BC = QR
` \=>frac{1}{2}BC=BM\ `[ BC median AM ]
` \=>frac{1}{2}QR=QN\ `[ QR median PN ]
we say,
BM = QN ` \-----(I)\ `
In ` \▵\ `ABM and ` \▵\ `PQN
AB = PQ[ Given ]
AM = PN[ Given ]
BM = QN[ From (I) ]
(i) ` \▵ABM≅▵PQN\ `[ Rule SSS ]
∠ABM = ∠PQN ` \-----(II)\ `[ CPCT ]
In ` \▵\ `ABC and ` \▵\ `PQR
AB = PQ[ Given ]
∠ABC = ∠PQR[ From (II) ]
BC = QR[ Given ]
(ii) ` \▵ABC≅▵PQR\ `[ Rule SAS ]
4. BE and CF are two equal altitude of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
solution :

Given,
BE ⊥ AC, FC ⊥ AB and BE = FC
Find,
AB = AC
In ` \▵\ `BEC and ` \▵\ `CFB
∠BEC = ∠CFB[ Given 90° ]
BE = CF [ Given ]
BC = BC [ Common ]
` \▵BEC≅▵CFB\ `[ Rule RHS ]
∠B = ∠C[ CPCT ]
AB = AC[ sides opposite to the equal angles ]
So, we say that
the triangle ABC is isosceles.
5. ABC is an isosceles triangle with AB = AC. Draw AP ⊥ BC to show that ∠B = ∠C.
solution :

Given,
AB = AC and AP ⊥ BC
Find,
∠B = ∠C
In ` \▵\ `APB and ` \▵\ `APC
AP = AP[ Common ]
∠APB = ∠APC[ Given 90° ]
AB = AC[ Given ]
` \▵APB≅▵APC\ `[ Rule RHS ]
∠B = ∠C[ CPCT ]




0 Comments